GPUによる数値計算
山梨大学大学院医学工学総合教育部 高木優一
総合情報処理センター 鈴木智博
目次
1.はじめに
2.GPU
3.GPGPU
4.CUDA
5.特異値分解
6.QR 分解
7.実験
8.考察・課題
1.はじめに
近年のグラフィックスプロセッサ(以下
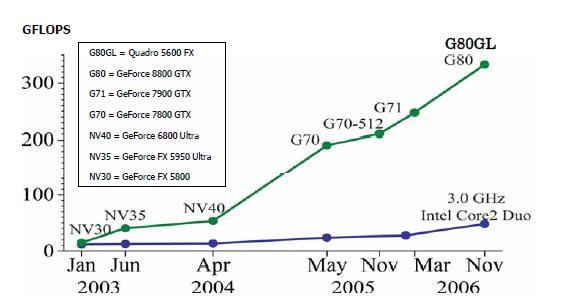
GPU)の性能向上は著しく理論ピーク性能が 500GFLOPS を超えるまでに成長している(図1).GPU
は本来グラフィックス処理専用のハードウェアであったがその処理能力の高さから汎用処理向けの研究が盛んに行われている.
一方,データマイニング,画像処理など広い分野で利用される数値線形代数アルゴリズムに特異値分解がある.各分野において扱う問題の大規模化に伴い,高速な実装が強く求められている.
本研究は現在データマイニングの分野などで需要の高い特異値分解をGPUによって高速化することを目的とした実験を行なった.
図1.GPUとCPUの性能推移[1]
2.GPU
ほとんどの GPU のハードウェアは現在 NVIDA 社と AMD 社の2大メーカによって作られている.GPU 内部には単純な計算を行う多数の演算装置がある.NVIDIA 社の GPU : Geforce8800GTX
は8基の演算装置を持つマルチプロセッサを16基備えており計128基の演算装置を持つ.これらの演算装置は数千のスレッドを走らせて並列処理を行うことが可能となっている.現段階での製品では単精度の浮動小数点演算しか扱うことが出
来ないが2008年度中には倍精度浮動小数点演算がサポートされる予定である.
GPU を使う際の注意点としてオーバーヘッドを考慮しなければならない.GPU
で演算を行うにはコンピュータのメインメモリから GPU メモリへデータ転送を行い演算結果を GPU
メモリからメインメモリへ転送しなければならない.行列サイズ 5000×5000 の行列積における実験では全演算時間が 2.84
秒,そのうちメモリ転送時間が 0.19
秒でありメモリ転送時間が全体の約7%を占めている.行列サイズが小さくなるほど演算時間に対してメモリ転送の割合が増えるため一定以下のサイズでは
GPU で演算させるより CPU で演算させた方が良い.
3.GPGPU
以前の GPU ハードウェアのアーキテクチャは固定パイプラインで構成されていたためグラフィックス以外の用途に使われる事はなかった。しかし2001年
にプログラマブルシェーダと呼ばれるソフトウェアで制御可能なアーキテクチャが登場し専用の言語を用いることで以前より幅広い処理を行えるようになった.
この時点ではまだ固定小数点型の演算しか行うことが出来ず汎用処理装置としての注目度は低かったが,2003年に単精度浮動小数点がサポートされるように
なりこの頃からの GPU の著しい処理能力の向上も伴い GPU で汎用処理を試みる研究が盛んに行われるようになった.これらのことを General
Purpose GPU(GPGPU) と呼ぶ.
現在までに報告された研究として FFT を14倍高速化した事例[1]や密度汎関数計算を高速化した事例[2]などがある.
4.CUDA
現在最新の NVIDIA 社の統合型シェーダをサポートする GPU では NVIDIA
社が無償で提供している汎用処理向け統合開発環境 CUDA[1] によりC言語でプログラミングを行う事が出来る.ここではC言語にはない CUDA における並列処理と共有変数の使用法について紹介する.
(1)並列処理
CUDAの処理単位として Grid,Block,Thread の三種類がある.
・Grid
CPU からGPU へ投げる処理単位.
・Block
GPU 内の各マルチプロセッサで処理される単位.
・Thread
マルチプロセッサ内で SIMD 演算される単位.
1Grid の中に複数の BLOCK が存在し,さらに各 BLOCK 中に多数の Thread が生成され並列処理を行う.
BLOCK 間の同期を取ることは出来ない. BLOCK 内の Thread では _syncthreads()_ 命令により同期を取ることが出来る.
(2)変数
変数の種類としてグロバール変数,共有変数がある.
・グローバル変数
GPUメモリに配置される変数でどの Block からでも参照できる.アクセス速度は遅い.
型名の前に_device_をつける. _device_ float alpha;
・共有変数
マルチプロセッサ内の共有メモリに配置される変数で Block 内の全スレッドでアクセス可能である.アクセス速度は速い.
型名の前に _shared_ をつける. _shard_ float beta;
ソースコードのうち,Thread 内で処理される部分を kernel コードと呼ぶ.変数 blockIdx によりブロック番号,threadIdx によりスレッド番号が取得出来る.これらの値により各スレッドが担当する並列処理部分を決定できる.
CPU 側のソースコードでは GPU のメモリ領域確保,メインメモリから GPU へのメモリ転送, BLOCK 数,Thread 数を指定して GPU 上にいくつのスレッドを走らせるか決定し CUDA で書かれた関数を呼び出す処理を記述する.
CUDA のプログラム例として Level1 BLAS の saxpy を挙げる.各スレッドが一要素分の計算を行う.CPU 側から GPU を呼び出す際,要素数=ブロック×スレッドとなるようにブロック数とスレッド数を決定する.
kernel コード
CPU コード
saxpy.tar.gz
5.特異値分解
特異値分解とは長方行列 A を A=UΣV'(Σ:対角行列 U,V:直交行列)に分解することである.Σ の対角要素を特異値と呼び U,V
を特異ベクトルと呼ぶ.これらはデータマイニングや画像処理などの分野で使われる基本的なアルゴリズムであり高速化が求められている.m×n 実長方行列の特異値は以下の手順で求めることが出来る.[3]
(1) A の QR 分解 O(mn^2)
(2) R の二重対角化 O(n^3)
(3) 二重対角行列の特異値分解 O(n^2)〜O(n^3)
(4) 逆変換 O(n^3)
(5) QR 分解の逆変換 O(mn^2)
大規模な問題においては m>>n であることが多く,計算量から分かるように,これらの中では A の QR 分解と QR 分解の逆変換に多くの時間が費やされる.今回はこのうち QR 分解の高速化を検討する.
6. QR 分解
QR 分解とは行列 A を A=QR(Q:直交行列,R:上三角行列)に分解することである.m×n(m>=n)行列 A
が列フルランクであるとき,m×n 直交行列 Q(Q' Q = I)と正の対角要素を持つ上三角行列
Rが一意に存在することが知られている.QR 分解の基本アルゴリズムは行列 A の各列に対して Gram-Schmidt
の直交化又はハウスホルダー変換をおこなうことにより得られる.
通常の計算プログラムは低速なメインメモリへのアクセスを控え,キャッシュなど高速なメモリできる限り使用するようチューニングされている.このような
チューニングをメモリアクセスの局所化という.メモリアクセスの局所化をプログラミングレベルで行う手法としてブロック化がある.扱う行列をいくつかの部
分行列(ブロック)に分割し,ブロック毎の演算を行うことでアクセスの局所化が行える.
単精度の QR 分解は LAPACK[4] では sgeqrf として実装されている.sgeqrf はブロック化 QR
分解アルゴリズムで実装されている.今回はこの関数内部の行列積部分をGPUで演算するようにプログラミングを行った.またブロック化 QR 分解の他に再帰
的 QR 分解[5]があるがこれについては今後実装予定である.
7.実験
実験環境を表1に示す.
表1.実験環境
| CPU | Core2duoE6600 |
| memory | 2G |
| GPU | Geforce8800GTX |
| GPUmemory | 768M |
| OS | Fedora7 |
| CPU_BLAS | GotoBLASv1.2.3 |
| GPU_BLAS | CU_BLASv1.1 |
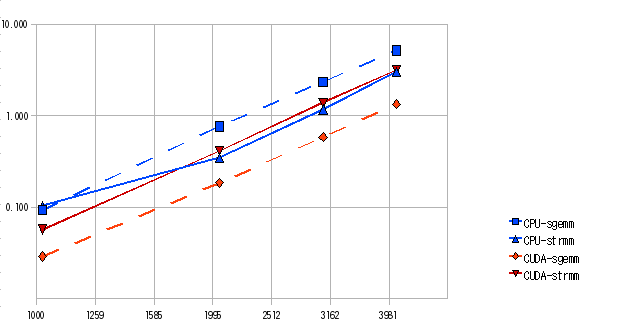
最初に CPU と GPU の行列積 C=AB の実行時間を測定した.結果を図2に示す.sgemm は単精度の一般行列同士の積を行い strmm は単精度の一般行列と三角行列の積を行う.
図2.strmmとgemmの実行時間
gemm では GPU が CPU の約5倍の演算速度で実行できており 100GFLOPS を超える処理性能を示している.strmm では GPU の性能がいまひとつであった.
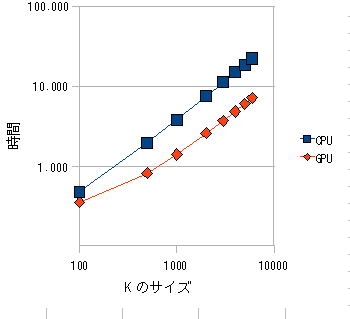
次に行列サイズを変化させた時の実行時間を比較する.A の行数 N と B の列数 M を 7000 に固定し A の列数 K
を変化させ時間を測定する.結果を図3に示す.K の値が十分に大きい場合は GPU の方が CPU より数倍速い結果となったが K の値が
100 では CPU と GPU で速度差がみられなかった.
図3.行列サイズによる比較
これらの結果を受け QR 分解内の sgemm 部分を GPU で演算し K が 100 以上であればGPUで実行することとする.
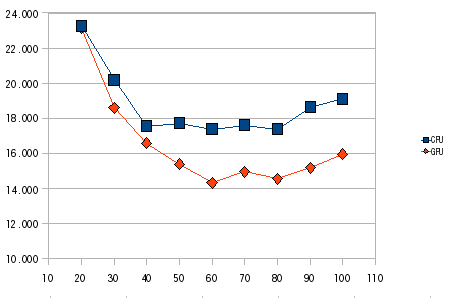
次にブロックサイズを変化させて最適なブロックサイズを求める.M=20000,N=3000 に固定しブロックサイズを 20〜100 の間を測定する.結果を図4に示す.
図4.ブロックサイズによる実行時間測定
この結果から CPU・GPU 共にブロックサイズを60に固定してM,Nを変えて実行時間の比較を行った.結果を表2に示す.
表2.QR 分解実行時間
| M×N | CPUのみ | GPUを並用 |
| 10000×1000 | 1.164 | 1.175 |
| 10000×2000 | 4.081 | 3.864 |
| 10000×3000 | 8.684 | 7.515 |
| 20000×1000 | 2.414 | 2.290 |
| 20000×2000 | 8.411 | 7.480 |
| 20000×3000 | 18.02 | 15.73 |
| 30000×1000 | 3.898 | 3.590 |
| 30000×2000 | 13.18 | 11.77 |
| 30000×3000 | 28.18 | 25.89 |
GPU を活用することにより最大で約13%の高速化が出来た.
8.考察・課題
最初の実験で GPU の strmm の性能があまり良くなかったがこれは CUDA の BLAS
実装のチューニングが進んでおらず今後性能向上するものと思われる.今回実装したブロック化 QR
分解では行列積の占める割合があまり多くなく最大13%程の高速化しか実現できなかった.これに対して再帰的 QR
分解では大部分を行列演算で実装することが出来る.再帰的 QR
分解においても同様の実験を行い性能を評価したい.この他特異値分解のステップ(5)の QR 分解の逆変換もO(mn^2) で QR
分解と並んで処理量の多い部分であるがこの部分も行列積がメインとなるため GPU で高速化が望めると思われる.
参考文献
[1]Nvidia
http://www.nvidia.com/
[2]安田耕二 グラフィックボードによる密度汎関数計算の加速 IPSJ Symposium Series Vol.2008,No2 p52 (2008)
[3]Demmel,J.W AppliedNumericalLinearAlgebra, SIAM,Philadelph ia (1997).
[4]Linear Algebra PACKage
http://www.netlib.org/lapack/
[5]Elmroth,E.and Gustavson,F Applying Recursion to Serial and Parallel
QR Factorization Leads to Better Performance,IBM Journal of Research
and Development,Vol.44,p.605(2000)