今回の出題された問題を例を使って説明する。

まずここに5つのベクトルがあるとする（横の系列）。それを以下の式によって二乗ノルムを計算する。

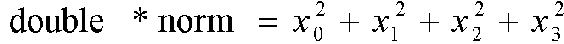
doubleは倍精度浮動小数点数を意味する。normが二乗ノルムである。上記の式はPSC'99実行委員会によって指定された式であってこれを守らないとソーティング結果が正答にならない。計算すると以下のような二乗ノルムが完成する。

ではこのベクトルと二乗ノルムからまず一番小さい値を取り出そう。一番小さい二乗ノルムがどれかを探す。すると30が一番normの中で一番小さい値になる。そこでベクトル２を一番としこの表の先頭の行に移動させる。

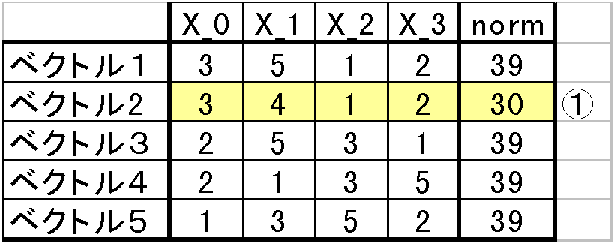
次に小さい値を見てみよう。ではベクトル２以外でnormが小さいものを探す。

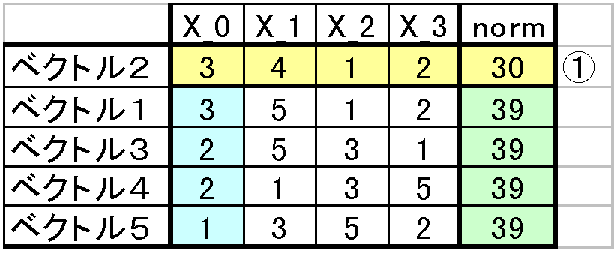
するとnormが39のベクトルが4つ、要するにベクトル２以外のベクトルはnormが39ということである。その場合ベクトルの成分を添え字の小さいもの同士を比較して小さい数値のほうを選ぶ。
ではX_0の添え字をベクトル１・３・４・５で比較してみよう。
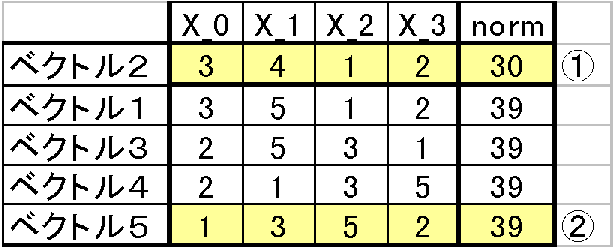
X_0の値の比較をした結果ベクトル５のX_0が１で一番小さかった。これによりベクトル達の中で二番目に小さいベクトルはベクトル５である事が分かったのでベクトル５をベクトル２の次の行に移動させる。

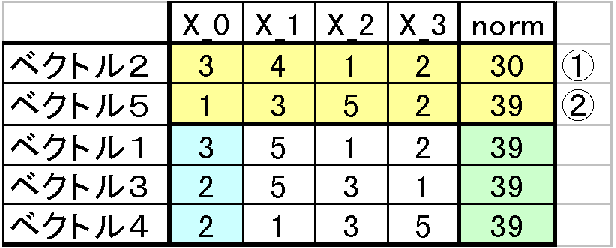
さあ、今度は残りの3つのベクトルから次に小さいベクトルを探す。先ほどと同じように残りのnormがすべて39である。そこでX_0をこの3つのベクトルで比較する。
見てみるとこの3つのベクトルでX_0が最小なものは2なのだが、二つのベクトルがX_0=2となっている。この様な場合はこの二つの中でX_1の値を比較して小さい数値のほうを選ぶ。

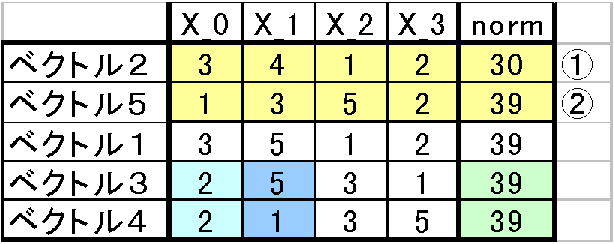
X_0=2であった二つのベクトルの中でX_1が小さいほうはベクトル４のX_1=1であることが分かる。

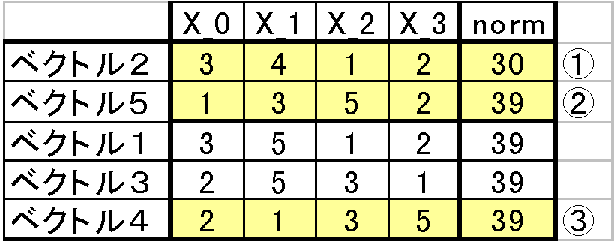
これにより3番目に小さいベクトルはベクトル４となるのでベクトル５の下にベクトル４を移動する。

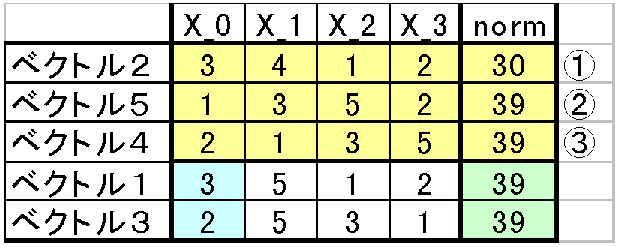
残りの二つに中で小さいベクトルを選ぶ。先ほどと同じようにnormは39で同じである。だからX_0を比較する。

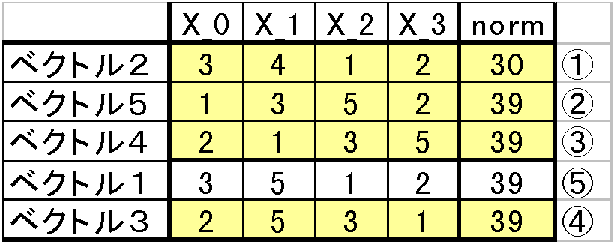
X_0を比較したらベクトル３のほうがX_0=2で小さいので、この二つのベクトルで小さいのはベクトル３だということが分かる。そこでベクトル３を４番目に小さいベクトルにしてベクトル４の下に移動する

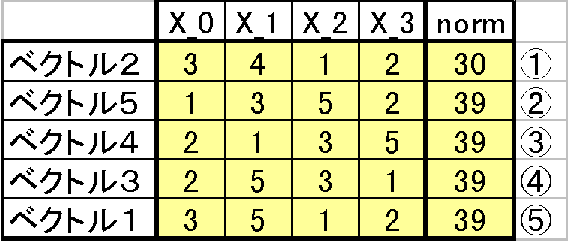
小さい順番にベクトル２・５・４・３と決まったのでこれで一番大きいベクトルがベクトル１と分かる。これでソーティングが終わる。実際の問題はこのベクトル成分が整数ではなく倍精度浮動小数点数になる。
これが今回の問題が私たちに作ってほしいプログラムの基本的な振る舞いである。